Edge-Weighted Graph에서의 최단경로를 찾는 Dijkstra Algorithm
그래프 G 상에서 vertex u에서 v로의 가장 짧은 path의 길이를 찾는 문제를 최단경로 문제라고 한다.
최단 경로 문제는 주로 1️⃣ edge에 weight가 존재하는지 2️⃣ edge weight 범위가 0이상인지/정수인지 3️⃣ 특정 vertex u에서 도달 가능한 path만 구하는지/모든 vertex set에 대해 구하는지 에 따라 사용할 알고리즘을 정하게 된다.
그 중 Dijkstra Algorithm은 edge에 weight가 존재하면서, 범위가 0 이상 이고 특정 vertex u에서 도달 가능한 vertex들의path를 구할 때 사용하는 알고리즘이다.
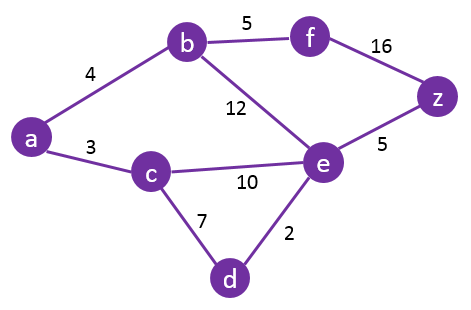

위 그림과 같은 형태에서 vertex f -> d로의 path는 여러 형태가 존재할 수 있지만, shotest path는 f-b-a-c-d(19)로 유일하다.
이를 구현하기 위한 다익스트라 알고리즘의 idea는 다음과 같다.
Dijkstra algorithm: Vertex u에서 graph G의 모든 다른 vertex 간의 shortest path의 길이를 계산한다.
- graph의 vertex들을 방문하면서 vertex u에서 다른 모든 vertex까지의 shortest path의 길이를 지속적으로 업데이트 한다.
- 처음에는 vertex u에서 u까지의 path의 길이는 0, 나머지는 무한대(INF)로 둔다.
| Vertex | vertex u에서 해당 vertex까지 shortest path의 길이 | vertex 방문 여부 |
| 0(시작 vertex라고 가정) | 0 | X |
| 1 | ∞ | X |
| 2 | ∞ | X |
| ... | ∞ | X |
| N | ∞ | X |
이후 Relaxation 과정을 거친다.
- 현재 방문 안 한 vertex들 중 현재 저장된 u에서의 shortest path의 길이가 가장 짧은 vertex v를 방문한다.
- 현재 vertex u에서 v를 제외한 나머지 모든 방문하지 않은 vertex w에 대해 vertex u에서 w까지의 shortest path의 길이를
- 1️⃣ 현재 u에서 w까지의 shortest path 길이
- 2️⃣ (u에서 v까지의 shortest path 길이) + edge (v, w)의 weight(해당 edge 존재시)
- 1️⃣과 2️⃣ 중 작은 값으로 update

| Vertex | vertex u에서 해당 vertex까지 shortest path의 길이 | vertex 방문 여부 |
| f | 0 | X |
| b | 5 = min of ∞ and 0+5 | X |
| z | 16 | X |
| ... | ∞ | X |
| N | ∞ | X |
위의 그래프에서는 시작 vertex f와 incident한 vertex b와 z에 대해 shortest path길이의 update가 발생했다.
이 때,
Key Lemma:
Dijkstra Algorithm에서 아직 방문 안한 vertex들 중 현재(저장된) vertex u에서부터의 shortest path 길이가 가장 짧은 vertex를 v라 하면 그 길이는 실제 u에서 v로의 shortest path의 길이와 같다.
(v를 방문하면 u-v까지의 shortest path의 길이가 확정된다)
가 성립한다.
즉, 위의 형태에서는 f를 방문한 뒤 vertex b로의 path 길이가 가장 짧다. 이것이 곧 vertex f에서 b로의 실제 shortest path 길이와 같다는 것 이다.
다익스트라 알고리즘 증명

👉 Base case:
처음 step에서는 무조건 vertex u(시작 vertex)를 고른다(나머지 vertex로의 distance는 무한대).
모든 edge의 weight가 0 이상이므로 vertex u에서 u까지의 제일 짧은 거리는 0보다 작을 수 없음
👉 Common Case:
위의 Lemma가 거짓이 아니라고 가정하고, 그것이 성립하지 않음을 통해 실질적으로 참임을 증명하는 귀류법을 사용한다.
Vertex v를 방문할 시 현재 저장된 u에서 v로의 path를 P라 하고, 이보다 더 짧은 path P'이 있다고 가정하자.
이 때, 경로 P'에서 v 직전에 방문하는 정점을 v'이라고 한다. 다익스트라 알고리즘이 수행되면서 v보다 v'를 먼저 방문하고, v'와 v가 인접하므로 P'의 길이가 최단 경로로 저장된다.
따라서 v' 다음으로 v를 방문할 때 에는 경로 P의 길이가 u - v 사이의 최단경로로 업데이트 되지 않는다 ❗❗
Lemma가 거짓이라고 가정할 때 모순이 발생하므로, Lemma "방문하지 않은 정점들 중 최단 경로가 가장 짧은 정점 v를 방문할 때의 길이는 실제 최단 경로와 같다"는 참이다
Dijkstra's Algorithm Pseudocode
procedure Dijjkstra(G, u, v):
Input: u and v is vertex in V(G),
Output: find path and cost from u to v
for all U ∈ V:
dist(U) = INF
dist(u) = 0
H = makequeue(V) (priority queue, using edge-weight as keys)
while H is not empty:
cost, node = deletemin(H)
for edge {cur, next} ∈ E:
if dist(cur) + w(cur, next) < dist(next):
dist(next) = dist(cur) + w(cur, next)
insert(H, next)