자료구조 Heap(힙)이란? 기본 연산과 HeapSort, Heapify에 대해

Heap은 자료구조의 한 종류로써,

특정 property를 만족하는 Complete Binary Tree를 말한다

Heap의 어떤 node p에 대해, p의 parent node를 q라 하면 q의 value는 p의 value보다 작다 ❗❗

이런 property를 만족하는 힙은 Min-Heap이라고 하며, 반대(q.value>p.value)의 경우에는 Max-Heap이라고 한다

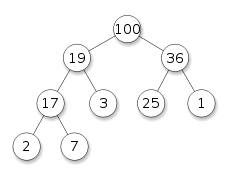
max heap - 출처 : https://en.wikipedia.org/wiki/Heap_(data_structure)

Heap은 보통 Priority Queue 혹은 Heap Sort를 구현하는데에 사용된다

그리고 Complete Binary Tree의 한 종류이기 때문에, Linked List보다는 Array로 구현하는 것이 효율적이다 😉

(중간에 낭비되는 공간이 없기 때문)

 

이 때, Heap의 대표적인 연산은 min(max)반환/insert/delete가 있다(연산의 설명에서는 max-heap이라 가정한다)

 

1️⃣ min(max)반환: Heap의 root node의 value를 반환한다

Heap에서 모든 child의 value는 자신의 parent의 value보다 작으므로, parent가 없는 root node의 value가 최대값임이 보장된다

시간복잡도: O(1)

 

2️⃣ Insert(value): Heap에 priority가 value인 node를 추가한다

힙은 완전이진트리이기 때문에 우선 맨 마지막 노드로 추가해준다

그리고, Heap의 Property를 유지하기 위해(parent의 value는 child의 value보다 작다)

- parent와 child의 priority를 비교해준 뒤, property에 어긋난다면 둘의 value를 교환해준다

- 성질을 유지할 때 까지 재귀적으로(parent로 이동) 해결해준다

시간복잡도: O(log n)

 

3️⃣ Delete(): Heap의 priority가 제일 큰(힙의 루트) 노드를 삭제한다

이 때, 2번과 마찬가지로 완전이진트리의 특성을 유지하기 위해 루트 노드를 맨 마지막 노드로 교체해준다(마지막 노드는 삭제)

마찬가지로 Heap의 property를 유지하기 위해,

- 현재 노드(p)와 left, right child중 priority가 큰 child를 선택한다

- p보다 child의 priority가 크다면, p와 child를 교체한다

- 만약 교체했다면, 현재 노드를 교체된 p(child로)로 변경한 뒤, 처음으로 돌아가서 재귀적으로 해결한다. 교체하지 않았다면 종료한다

시간복잡도: O(log n)

#define MAX_SIZE (1<<5)
typedef struct heap {
	int array[MAX_SIZE];
	int cur;
}heap;

void create(heap* h) {
	h->cur = 0;
}

int isEmpty(heap* h) {
	if (h->cur > 0)return 0;
	return 1;
}

int findmax(heap* h) {
	return h->array[0];
}

void insert(heap* h, int item) {
	if (h->cur < MAX_SIZE) {
		h->array[h->cur] = item;

		int temp;
		int parent = (h->cur - 1) / 2;
		int index = h->cur;

		while (parent >= 0) {
			if (h->array[parent] < h->array[index]) {
				temp = h->array[parent];
				h->array[parent] = h->array[index];
				h->array[index] = temp;
				index = parent;
				parent = (index - 1) / 2;
			}
			else break;
		}
		h->cur++;
	}
}

int deletemax(heap* h) {
	if (isEmpty(h))return -1;
	int value = h->array[0];
	int new_root = h->array[h->cur - 1];
	h->array[h->cur - 1] = 0;
	h->array[0] = new_root;
	h->cur--;

	int index = 0, max;
	int left = 1,right=2,temp;
	while (left < h->cur || right < h->cur) {
		max = index;
		if (left < h->cur && (h->array[left] > h->array[max]))
			max = left;
		if (right < h->cur && (h->array[right] > h->array[max]))
			max = right;

		if (max != index) {
			temp = h->array[max];
			h->array[max] = h->array[index];
			h->array[index] = temp;

			index = max;
			left = index * 2 + 1; right = index * 2 + 2;
		}
		else break;
	}

	return value;
}

heap의 구현은 위와 같이 가능하다

 

이렇게 우선순위가 가장 높은 value를 반환하는 Heap의 특성을 이용해서 Priority Queue를 구현할 수 있다🤔

그러면 N개의 node를 가진 Heap에서, N개를 pop하면 priority순으로 value를 정렬할 수 있다 ❗❗

이 때의 시간복잡도는 N개의 node * delete연산 = O(n log n)이고, 이를 Heap Sort라 한다

 

int* heapSort(heap* h) {
	int* arr = (int*)malloc(sizeof(int) * (h->cur+1));
	int index = 0;
	while (h->cur != 0) {
		arr[index] = deletemax(h);
		index++;
	}
	return arr;
}

 

HeapSort는 Worst-Case에서도 O(n log n)의 시간복잡도를 유지할 수 있지만, Heap을 생성하기 위한 공간이 필요하다

하지만 Heapify 연산을 이용하면, 추가 array를 생성하지 않고서도 정렬 가능하다

 

Heapify: 모든 non-leaf node인 p에 대해 level order의 역순으로 node p와 p의 child 중 작은 값(min-heap)을 가진 node가 heap property를 만족할 때 까지 계속해서 swap한다

Heapify 연산의 순서는 다음과 같다(배열 이름을 A라 가정, Heap은 Min Heap)

1️⃣ A를 완전 이진 트리(힙)의 순서에 맞게 트리에 대응하여 생성

2️⃣ Level Order의 역순으로 탐색을 진행한다(index: N/2 -1 ~ 0)

3️⃣ 현재 p의 두 child 중 작은 값을 가진 node가 heap property를 만족하지 않는다면 swap

4️⃣ 3번에서 swap했다면 p를 child로 바꾼 뒤 3번으로 다시 돌아간다

 

연산을 모두 수행하게 되면 A는 Heap이 완성된다 

5️⃣ Heap에서 delete 연산을 N번 진행한다

6️⃣ 현재 index를 i라고 할 때, delete하여 얻어낸 min값을 A[n-i]에 덮어씌우기

 

5,6번을 N번 진행하고 나면 배열은 내림차순으로 정렬된다 

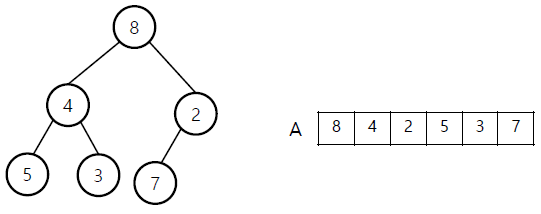
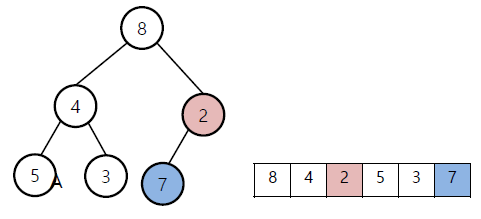
왼: 초기상황 / 오: level이 h-1인 node중 가장 마지막인 2와 child 7 비교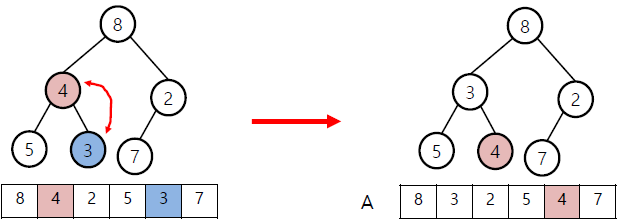

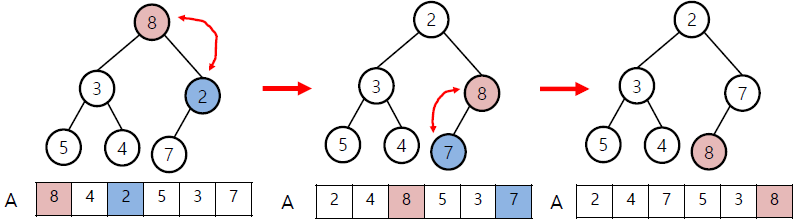
왼: 다음 node인 4와 child중 작은 node인 3 비교 후 swap / 오: 8과 2 swap, 8과 7 swap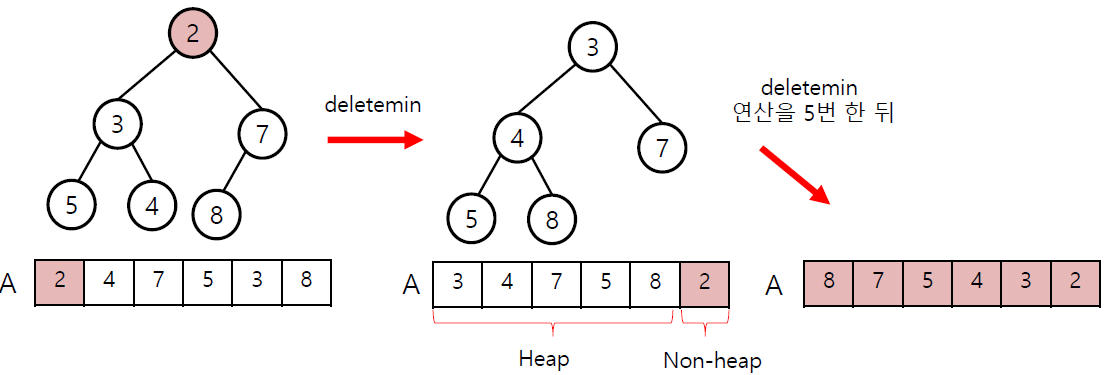

delete 연산을 n번 수행한 뒤

Heapify 연산을 완료한 뒤 delete연산을 n번 수행하면, min-heap은 내림차순, max-heap은 오름차순 정렬이 완료된다

 

이 때, Heapify 연산을 level order의 역순으로 진행하는 이유는 뭘까? 🤔

heapify 연산 중 3,4 번이 level 오름차순으로 진행되기 때문에, 만약 level order 순으로 진행한다면 swap이 제대로 진행될 수 없다

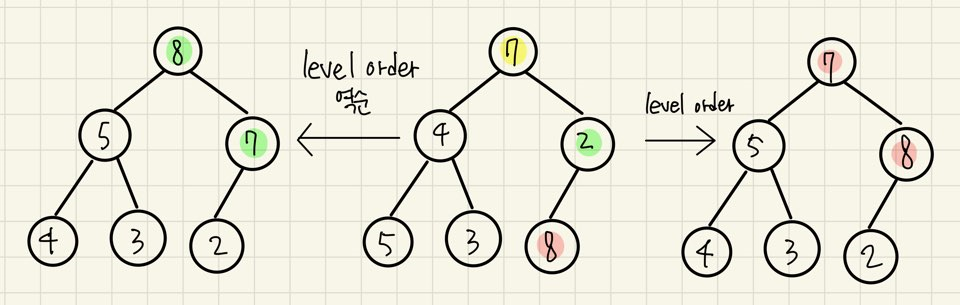
이 사진에서도 level order 순으로 heapify를 진행하게 된다면(max heap), 

맨 처음 7과 2를 비교한 뒤 swap하지 않고, 마지막에 2와 8을 한번만 swap하기 때문에 heap property가 성립하지 않는다

정확하게는, Heapify 연산을 하면서 특정 노드에서 depth가 증가하는 순으로 비교와 swap을 진행한다.

그래서 root node(Max값)는 swap될  기회가 한 번 밖에 없다. 만약 level order 순으로 진행한다고 가정해도, 나중에 진짜 max값이 위로 올라오더라도 root node로 swap될 수 없기 때문에 heap property를 만족하지 않는다. (한번의 비교시 최대 한 칸 올라올 수 잇기 때문에 depth가 높은 노드가 root까지 올라오기 위해서는 level order 역순의 진행이 필요하다)