Array의 k번째 작은 element 찾기 - QuickSelect 알고리즘

Size가 n인 int형 Array에서 k번째로 작은 element를 찾는 방법은 여러 가지가 있다.

가장 formal하게, 배열을 sort한 뒤 인덱스가 k인 element를 반환하면 간단하게 구할 수 있다.

우리가 알고있는 Sort 알고리즘의 시간 복잡도는 (효율적인 알고리즘 가정) O(n logn)인데, Sort 문제를 해결하면 손쉽게 Selection문제를 해결할 수 있다(이것을 Sort에서 Selection으로의 Reduction이 가능하다고 말한다)

 

그러면 Selection 문제는 O(n logn)내에 해결할 수 있는데, (이론적으로) 더 빠른 알고리즘이 있을까?

 

Divide And Conquer를 활용하고, Quick Sort와 유사하게 pivot을 지정함으로써 size가 n인 Int형 Array에서 k번째로 작은 element를 찾을 수 있다

이것을 Quick Select 알고리즘이라고 한다

 

(Quick Sort란?)

2jinishappy.tistory.com/75?category=903864

Quick Sort 정의, 알고리즘 및 코드에 대해

Quick Sort는 Array에서 pivot을 기준으로 정해서 배열을 divide하고 merge하는 방법을 반복하는 분할정복 정렬 알고리즘 중 하나이다

Quick Selection 또한 이 정렬 방식과 매우 유사하게 작동한다.

 

Quick Selection 알고리즘:

1️⃣ Array의 element 중 Random한 하나의 element를 pivot으로 정한다.

2️⃣ Array를 A1(Array의 element 중 pivot보다 작은 element들을 모은 Array)와, A2(〃 중 pivot보다 큰 element들을 모은 Array)로 partitoning 한다.

3️⃣ |A1|(A1의 배열 Size)에 따라, 다음의 세 가지 경우로 나뉜다

- k ≤ |A1| : k번째 작은 element가 A1 배열 내에 있는 경우. Input Array를 A1으로 정한 뒤 k번째 작은 element를 찾는 Subproblem의 값을 반환한다

- k = |A1| + 1 : A1의 size가 k-1개 이므로 자동으로 pivot이 k번째 작은 element가 된다. pivot 반환

- k > |A1| + 1 : k번째 작은 element가 A2 배열 내에 있는 경우. Input Array를 A2로 정한 뒤 k-(|A1|+1)번째 작은 element를 찾는 Subproblem의 값을 반환한다(A1과 pivot이 아니기 때문에).

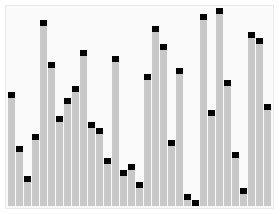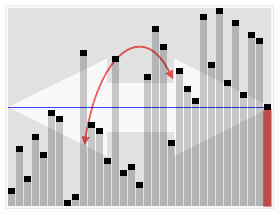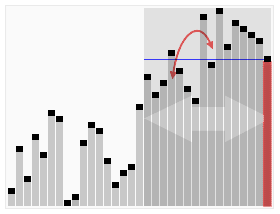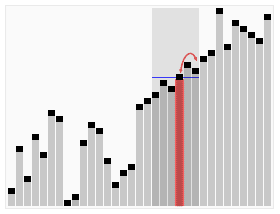
출처: 위키피디아

 

코드로 구현하면 아래와 같다

int quickSelect(vector<int> arr, int k) {
	int pivot = arr[0];	//임의의 element를 pivot으로 설정

	vector<int> A1, A2;

	for (auto x : arr) {
		//pivot을 기준으로 element partitioning
		if (x < pivot)
			A1.push_back(x);
		else if (x > pivot)
			A2.push_back(x);
	}

	if (k <= A1.size())	//찾고자 하는 answer가 A1에 있을 경우 subproblem 호출
		return quickSelect(A1, k);
	else if (k == A1.size() + 1)	//현재 problem의 answer가 pivot일 경우 반환
		return pivot;
	else 	// 찾고자 하는 answer가 A2에 있을 경우 subproblem 호출
		return quickSelect(A2, k - (A1.size() + 1));
}

간단한 알고리즘이고, 시간복잡도는 Quick Sort와 동일하지만 문제가 발생한다.

 

1

2

3

4

5

6

7

8

배열이 위와 같을 경우에는 quickSelection 함수를 호출할 때 마다,

A1의 size는 0이 되고 A2의 size는 n-1이 된다 (모든 element가 pivot인 첫 번째 element보다 크기 때문)

따라서 quickSelection을 N번 호출하고, partioning하는 데에 O(N)이 소모되기 때문에 Worst case의 Time complexity는 O(N²)가 된다

 

이런 편중을 막기 위해, pivot을 선정할 때

1️⃣ 각 element를 uniformly random하게 선택하고(모든 element 중 하나를 선택하면서, 그 확률이 전부 동일)

2️⃣ partitioning시 A1 or A2의 size가 하나라도 3n/4를 넘으면 1번으로 돌아가기

의 과정을 추가해준다. 이 때, 2번의 조건을 만족하지 않는 pivot(고르게 분할할 수 있는 pivot)을 good pivot이라 한다.

 

int quickSelect(vector<int> arr, int k) {
	double bound = ((double)arr.size()*3)/4;
	random_device rd;
	mt19937 gen(rd());
	uniform_int_distribution<int> dis(0, arr.size() - 1);

	while (1) {
		int pivot = arr[dis(gen)];	//uniformly randomize한 element를 pivot으로 설정
		vector<int> A1, A2;

		for (auto x : arr) {
			//pivot을 기준으로 element partitioning
			if (x < pivot)
				A1.push_back(x);
			else if (x > pivot)
				A2.push_back(x);
		}
		
		if (A1.size() > bound || A2.size() > bound)	//비균등하게 partitioning 되었을 경우
			continue;

		if (k <= A1.size())	//찾고자 하는 answer가 A1에 있을 경우 subproblem 호출
			return quickSelect(A1, k);
		else if (k == A1.size() + 1)	//현재 problem의 answer가 pivot일 경우 반환
			return pivot;
		else 	// 찾고자 하는 answer가 A2에 있을 경우 subproblem 호출
			return quickSelect(A2, k - (A1.size() + 1));
	}
}

이 경우에는 평균적으로 2번의 시도 안에 good pivot을 구할 수 있다(bad pivot의 범위는 array size의 절반이기 때문).

또한 subproblem의 크기는 최대 3n/4로 제한된다.

 

T(n)을 quick selection 알고리즘에 소모되는 average(expected) time이라 했을 때,

T(n) ≤ T(3n/4) + O(n)이 되고, master theorem에 의해 T(n) = O(n)이 된다 🤗

 

이처럼, Quick Selection의 성능은 Good pivot을 얼마나 빠르게 찾는가에 달렸다.

다음 포스팅에서는 good pivot을 worst-case O(n)에 찾는 알고리즘인 median of medians에 대해 알아본다.

⏬

2jinishappy.tistory.com/127

Quick Select를 O(n)에 구현 가능한 Median of Medians 알고리즘