방향 그래프에서 사이클의 집합 Strongly Connected Component

이전에 Biconnected Component와 Cut Vertex에 대해 포스팅한 적이 있다

https://2jinishappy.tistory.com/169?category=903864 

무방향그래프에서의 Cut Vertex와 Biconnected Components

간단히 요약하자면

Cut Vertex: Connected Undirected Graph에서 특정 정점을 제거했을 때 2개 이상의 Connected Component로 분리되게 하는 Vertex

Biconnected Component: Connected Undirected Graph에서 1️⃣Connected 하면서 2️⃣Cut Vertex가 존재하지 않는 Componenet Set ➡ Biconnected Component 내의 임의의 vertex u,v는 항상 path를 지님 ➡ 사이클이 존재

 

이처럼 Biconnected Component는 Connected Undirected Graph에서 정의되었다

Strongly Connected Component(이하 SCC)는 Directed Graph에서 connectivity를 보이기 위한 자료구조이다.

 

Strongly Connected: 임의의 서로 다른 두 vertex v, w ∈ V(G)에 대해 v에서 w로의 path와 w에서 v로의 path가 존재한다

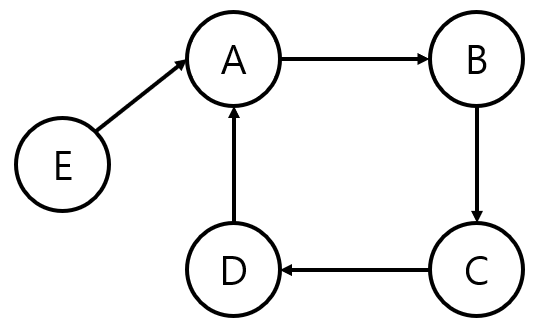
왼: strongly connected / 오: Not strongly connected

왼쪽 그래프(파란 선은 실제 간선이 아니다)을 봤을 때, A에서 출발해서 다른 모든 정점인 B,C,D로의 path가 존재한다. 그리고 다른 모든 정점인 B,C,D에 대해서도 성립하므로 strongly connected 하다.

하지만 오른쪽 그래프는 E에서 A,B,C,D로의 path가 존재하지만 다른 정점에서 E로 가는 path가 존재하지 않기 때문에 strongly connected하지 않다.

 

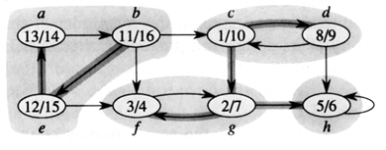
출처: https://www.acmicpc.net/problem/2150

Strongly Connected Component of G : G의 maximal strongly connected subgraph

 

따라서 우리의 주 관심사는 Connected Graph G가 주어졌을 때 G의 vertex들을 partitioning하는 모든 Strongly Connected Component를 찾는 일이 될 것이다 (그리고 Biconnected Component와 마찬가지로 SCC는 vertex의 cycle 집합이다)

 

정답부터 말하자면 SCC를 구하는 데에는 두 번의 DFS면 가능하다 😮

 

우선 SCC를 구하기 전에, 방향그래프 G에서 모든 edge들의 방향을 뒤집은 그래프 R이 필요하다

왼: 기존 그래프 G / 오: edge들의 방향을 뒤집은 그래프 R

 

일단 러프한 방법으로 SCC를 구해보자

1️⃣ 각 vertex v에 대해 G와 R로부터 DFS 수행

👉 G에서 v로부터 reachable한 vertex set을 S1, R에서 v로부터 reachable한 vertex set을 S2라 하자

• S = S1∩S2에 속한 vertex는 G의 SCC를 이룬다
• why? S에 속한 임의의 vertex를 u, w라 할 때, S의 정의에 의해 ⓐv에서 u로의 path(G) ⓑu에서 v로의 path(R) ⓒv에서 w로의 path(G) ⓓv에서 w로의 path(R)가 존재한다.
• ⓑ와 ⓒ로 인해(u ➡ v ➡ w) u에서 w로의 path가 존재한다
• ⓐ와 ⓓ로 인해(w ➡ v ➡ u) w에서 u로의 path가 존재한다

SCC에 속한 vertex는 모두 서로간의 path가 존재하므로 이 방식을 이용하여 SCC를 구할 수 있다

이 때 time complexity는 

• R구하기 = O(n+m)
• 모든 vertex에 대해 G와 R에서 DFS 수행 = n * O(n+m) = O(n(n+m))

이므로 O(n(n+m)) 이다

 

하지만 두 번째 방법을 이용하면(두 번의 DFS) 더 빠르게 SCC를 찾을 수 있다 ~_~

2️⃣ DAG 이용

(우선 DAG에 대한 이해가 필요하다면 아래의 링크를 참조하자)

https://2jinishappy.tistory.com/225?category=920680 

DAG - Directed Acyclic Graph

Directed Graph G에 대해, 각 SCC를 하나의 vertex로 가정하고 SCC S1에서 S2로 가는 edge가 존재하면, 해당 edge(S1, S2)를 추가하는 방식으로 생성한 그래프를 D라고 하자

위의 그래프 G를 변환한 그래프 D

위의 그래프를 서술한 방식을 통해 생성한 그래프 D는 DAG가 된다(D가 DAG가 아닐 경우 maximal condition 위배)

 

이 때 SCC를 구하기 위해 알아야 하는 중요한 프로퍼티는

D의 sink에 속한 아무 vertex를 선택해서 S에서 reachable node set을 구하면, D의 sink에 속한 모든 vertex(SCC)의 집합과 동일하다

는 것이다 !!

(위의 그래프에서 sink인 h에 속한 vertex(h)에서 dfs를 수행하면 하나의 SCC인 {h}를 반환한다)

 

그렇다면 두 가지 subproblem이 발생한다

1. D의 sink에 속한 vertex 중 하나를 어떻게 찾는가?
2. D의 sink에 해당하는 SCC를 찾은 이후, 나머지 SCC들은 어떻게 찾는가?

 

이것 또한 차근차근 살펴보자

🅰 D의 sink에 속한 vertex 중 하나를 어떻게 찾는가?

➡ D의 source에 속한 vertex 중 하나를 찾는 방법은 간단하다 ~!~!~!~!~!~!~!

• D의 두 vertex(G의 SCC) S1, S2에 대해 edge(S1, S2)가 있다면?
• G에서 DFS를 하면 S1의 highest post number(S1의 모든 vertex 중 post(v) 값이 제일 큰 vertex v)는 언제나 S2의 highest post number보다 크다
  • post number가 클 수록 topological order가 큰 것이므로 source에 가깝다 !!
• why?
  • S1에 있는 vertex v로부터 explore: (S1, S2)가 존재하므로 S2의 모든 vertex는 v에서부터 reachable하다(DFS tree에서 S1, S2의 모든 vertex가 v의 descendant가 된다)
  • S2에 있는 vertex u로부터 explore: u를 root로 가지는 트리는 S1의 어떤 vertex도 descendant로 가질 수 없다. 따라서 S2에 있는 vertex를 모두 방문한 뒤 S1에 있는 vertex를 explore하게 된다

 

따라서 D의 source는 G에서 highest post number를 가진 vertex를 무조건 포함하게 된다 ❗❗

👉 D와 G의 reverse 그래프 R을 변환한 그래프 Rd은 같은 vertex set을 가지고 있으며(같은 SCC를 공유), D의 sink는 Dr의 source와 같다

 

결과적으로, 

Rd에서 DFS를 한 뒤 highest post order를 가진 vertex (= Rd의 source에 속한 vertex)는 무조건 D의 sink에 속한다

 

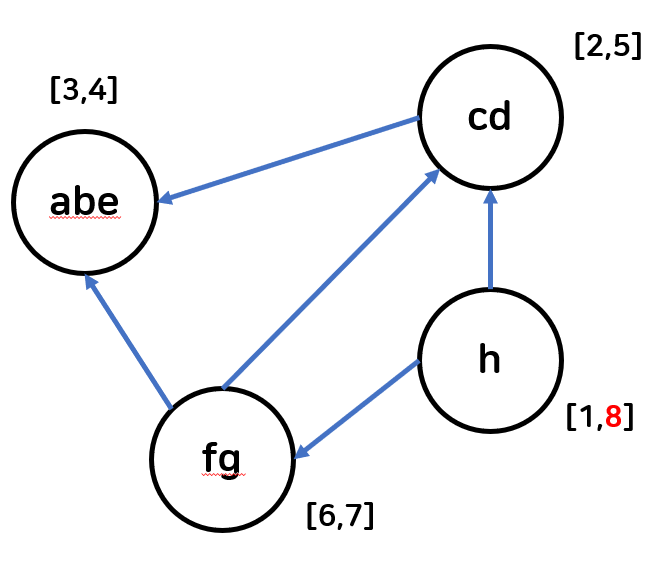
그래프 G의 edge를 reverse한 그래프에서 SCC를 하나의 정점으로 변환한 그래프 Rd

이 그래프에서도 Rd의 DFS를 통해 D의 sink에 속하는 vertex인 h를 찾아낼 수 있다 ~~

 

🅱 D의 sink에 해당하는 SCC를 찾은 이후, 나머지 SCC들은 어떻게 찾는가?

👉 Rd에서 source를 제거하고, 해당되는 vertex들을 G에서 모두 제거해도, 여전히 남아있는 vertex들 중에 가장 post number가 큰 vertex는 Rd의 source에 속해 있다

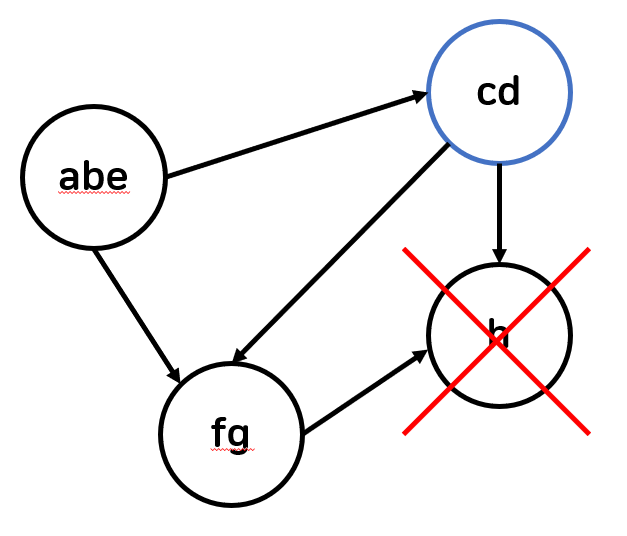
{h}를 삭제한 뒤 그래프 D의 상태

방금 D의 sink에 속하는 vertex set {h}를 모두 삭제했다. 이 때 D에서는 새로운 sink (CD)가 생기게 되고 그것은 즉 Rd에서도 새로운 source (CD)가 생긴다는 뜻이당

따라서 재귀적으로 

1. Rd에서 DFS를 수행하여 D의 sink에 속하는 vertex 탐색
2. (그래프 G상에서) 해당 vertex에서 reachable한 node들을 모두 제거하면서 SCC set에 추가

를 반복하면 SCC set를 찾을 수 있당

 

결과적으로 얻을 수 있는 SCC는 이것이다

 

수도코드는 아래와 같다 ~

do DFS(Gr) and sort vertices in decreasing post number
Mark all nodes as unvisited
for each u in the computed order do
	if u is not visited
    	then explore(u) on G
        Let Su be the nodes reached by u
        Output Su as a strongly connected Component
        Remove Su from G

 

 

---

개인적으로는 https://www.acmicpc.net/problem/4196 이 문제를 풀고 SCC가 굉장히 흥미있는 개념이라는걸 느꼈고

DFS 두 번으로 구할 수 있다는게 놀라웟다

 

엄청나게 어렵지만 재밌게 배웠던 P NP Problem에서, 대표적인 NP-Complete인 SAT problem 또한 SCC의 응용 알고리즘이라는걸 배웟고

3-SAT problem이 대부분의 NP-complete problem으로 reduction이 가능하다는걸 알고 나니 SCC 알고리즘이 굉장히 중요한 개념이라고 느꼈당

DFS -> SCC 알고리즘 -> 3-SAT prob -> NP-complete 로 진화해가는 과정이 ....

 

알고리즘의 세계는 너무나 어렵고 고단하지만 하나씩 배워가는 재미는 있는 것 같다 ... 그래도 괴물들 사이에서 버틸 자신이 없으니 대학원 안 가길 잘했다 ^^