[C++] Dijkstra Algorithm with Priority Queue

다익스트라 알고리즘은 가중치가 양수로만 이루어져 있는 무방향/방향 그래프에서 최단거리를 찾는 알고리즘이다

(unweighted 그래프의 경우는 BFS로 최단거리를 탐색 가능하다)

 

알고리즘은 다음과 같다🤗

 

1️⃣ 임의의 출발점 u에서부터 최단거리를 저장할 배열 dist[vertex]를 선언하고 dist[u]에는 0을, 다른 노드들에는 INF를 저장한다

2️⃣ 출발점 u를 현재 노드(cur)로 저장한다

3️⃣ cur와 인접한 노드(next)에 대해 dist[cur] + edge[cur][next]와 dist[next]를 비교한다

4️⃣ 둘 중 최솟값을 dist[next]에 갱신한다(INF일 경우 전자의 값으로 한다)

5️⃣ cur와 인접한 모든 노드에 대해 이 작업을 수행한다

6️⃣ cur의 상태 배열 visit[cur]을 true로 바꾼다(방문 체크한다)

7️⃣ visit[false]인 모든 노드들 중 dist의 값이 최소인 노드를 cur로 정한다(이 때 새로운 cur에 대해 dist[cur]은 u로부터 cur까지의 실제 최단거리이다)

8️⃣ 도착점 v에 방문을 완료했거나 더이상 방문 가능한 노드가 없을 때 까지 3️⃣~ 7️⃣번을 반복한다

 

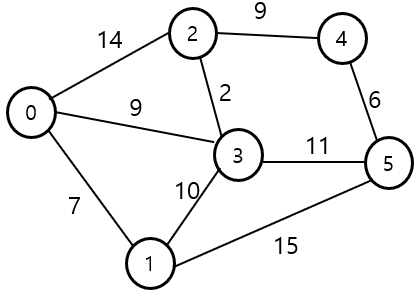
입력값이 👇 아래의 형식과 같을 때 다익스트라 알고리즘을 활용한 최단거리 알고리즘 구현 코드

0 4
9
0 1 7
0 2 14
0 3 9
1 3 10
1 5 15
2 3 2
2 4 9
3 5 11
4 5 6

#include <cstdio>
#include <cstring>
#define VERTEX 6
#define INF 987654321
int edge[VERTEX][VERTEX], e, u, v;
bool visit[VERTEX];
int dijkstra(int u, int v) {
	int cur = u, min;
	int dist[VERTEX] = { 0 };
	memset(visit, false, sizeof(visit));
	for (int i = 0; i < VERTEX; i++)
		if (i == u)dist[i] = 0;	//출발점에서의 거리는 0
		else dist[i] = INF;	//다른 점들은 최대값 저장
	do {
		min = INF;
		for (int next = 0; next < VERTEX; next++) {
			if (!edge[cur][next] || visit[next])continue;
			//연결돼있지 않거나 이미 방문한 노드이면

			if (dist[cur] + edge[cur][next] < dist[next])
				dist[next] = dist[cur] + edge[cur][next];
			//거리 비교 후 최소값 갱신
		}
		for (int next = 0; next < VERTEX; next++) {
			if (visit[next])continue;
			if (min == INF)min = next;
			else
				min = dist[next] < dist[min] ? next : min;
			//시작 노드에서 최소 거리인 다음 노드 찾기
		}
		visit[cur] = true;	//방문 체크
		cur = min;	//최소 거리인 노드를 다음 탐색 노드로 갱신

		if (visit[v])
			return dist[v];
		//도착점 v로의 최단거리 계산이 완료된 경우
	} while (min != INF);	//더이상 방문할 수 있는 노드가 없을 때 까지

	return -1;	//u에서 v로의 경로가 없는 경우
}
int main() {
	scanf("%d%d", &u, &v);
	scanf("%d", &e);
	for (int i = 0, a, b, w; i < e; i++) {
		scanf("%d%d%d", &a, &b, &w);
		edge[a][b] = edge[b][a] = w;
		//방향그래프일 경우 edge[b][a]에는 삽입하지 않으면 됨
	}

	printf("%d", dijkstra(u, v));
	//u에서 v로의 최단경로 출력
	return 0;
}

시간복잡도: O(V^2)

하지만 위와 같은 경우는 O(n^2)의 시간복잡도를 요구하기 때문에

우선순위큐를 응용해서도 다익스트라 알고리즘을 구현 가능하다

#include <cstdio>
#include <queue>
#include <vector>
#define VERTEX 6
#define INF 987654321
using namespace std;

int edge[VERTEX][VERTEX], e, u, v;
bool visit[VERTEX];
int dijkstra(int u, int v) {
	vector<int> dist(VERTEX + 1, INF);
	priority_queue<pair<int, int>> pq;

	pq.push({ 0,u });
	dist[u] = 0;
	//출발점에서의 거리는 0

	while (!pq.empty()) {
		int cost = -pq.top().first;	//다음 최소 거리
		int cur = pq.top().second;	//거리가 최소인 노드

		pq.pop();

		for (int next = 0; next < VERTEX; next++) {
			if (!edge[cur][next])continue;
			int ncost = edge[cur][next];

			if (dist[cur] + ncost < dist[next]) {
				dist[next] = dist[cur] + ncost;
				pq.push({ -dist[next],next });
				//거리가 작은 순으로 우선순위 부여
			}
			//거리 비교 후 최소값 갱신
			
		}
	}
	return dist[v];
	//목적지 v로의 거리 반환
}
int main() {
	scanf("%d%d", &u, &v);
	scanf("%d", &e);
	for (int i = 0, a, b, w; i < e; i++) {
		scanf("%d%d%d", &a, &b, &w);
		edge[a][b] = edge[b][a] = w;
		//방향그래프일 경우 edge[b][a]에는 삽입하지 않으면 됨
	}

	printf("%d", dijkstra(u, v));
	//u에서 v로의 최단경로 출력
	return 0;
}

시간복잡도: O(V+E log V)