Divide-and-Conquer 알고리즘과 Master Theorem

Divide and Conquer는 분할 정복이라고 한다

구체적으로는

 

1️⃣ 주어진 문제를 작은 subproblem으로 쪼갠다 (subproblem이란? 본 문제와 같은 로직이지만, input size가 작은 문제)

-> Divide

2️⃣ 나눈 subproblem들을 Recursively하게 해결한다

3️⃣ 2번에서 푼 subproblem들의 답을 적절하게 조합(combine, merge)해서 원래의 답을 도출한다

-> Conquer

 

분할 정복 알고리즘의 대표적인 예시로는 Merge Sort가 있다

divide

위의 그림은 A라는 큰 배열을 작은 subproblem으로 나눈 것이다

한 번 나눌 때마다 input size는 2분의 1배가 되므로, divide하는데에는 O(log n)이 소모된다

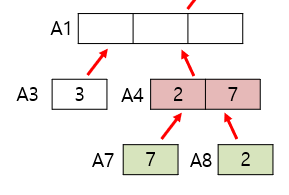
전 후

첫 번째 사진에서 A7과 A8을 merge한 결과가 A4에 반영된다

합칠 때는 A7과 A8을 처음부터 순회하면서 현재 가리키고 있는 두 값을 비교한 뒤, 작은(또는 큰) 값을 push하고, 인덱스를 증가시키면 된다

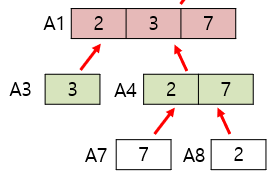
두 번째 사진에서도 A3과 A4를 merge하면 A1이 나온다

모든 subproblem에 대해, merge연산은 총 N번 시행한다

merge한 결과

그러면 해당 알고리즘의 시간복잡도는 어떻게 될까?

위에서 구한 것 처럼, input size가 2분의 1로 되게끔 subproblem을 나눈 뒤 merge하는 과정을 반복한다

이 때 Time Complexity를 T(n)이라 하면 T(n) = 2*T(n/2) + O(n)이라고 할 수 있다.

 

이와 같이 subproblem이 n/b의 형태를 띨 때에 한해서,

size가 n/b인 a개의 subproblem으로 나눠지며 답을 merge할 때 O(n^d)시간이 걸릴 경우 일반식을 도출해낼 수 있다

T(n) = a*T(n/b) + O(n^d) - Master Theorem

또한 위의 일반해에서 시간복잡도는 다음과 같이 구할 수 있다

예를 들면, T(n) = 5(n/2) + O(n^2)일 때, 2 < log2(5)이므로 T(n)의 시간복잡도는 O(n^log2(5))이다

 

 

 

출처 - 충북대학교 소프트웨어학과 알고리즘 강의자료