-
Sort Algorithm(Bubble/Insert/Selection/Merge/Quick)과 시간복잡도Algorithm 2021. 2. 25. 15:18
1. Bubble Sort
: 인접한 원소끼리 대소를 비교하고 swap시켜 unsorted part중 가장 작은(sort priority가) element를 sorted part의 직전에 위치시키는 정렬
bubbleSort(A[1 ... N], N): for i in [1 ... N]: for j in [1 ... N-i]: if A[j] > A[j+1]: swap A[j] and A[j+1]- bubble sort의 validaity: i번째 stage 후에 Array에서 i번째로 큰 값은 항상 A[n-1-i]번째에 위치하게 된다(loof invariant). 즉, 정렬되어 위치해야 할 올바른 위치에 자리잡게 된다.
- time complexity: O(N²)
- i번째 stage에서 가장 큰 element를 sorted part로 보내는 과정에서 비교 연산을 N-1-i번 수행한다
- Array의 크기를 N이라 할 때 N-1번의 stage를 수행한다
2. Selection Sort
: unsorted part에서 가장 큰(sort priority) element를 찾아 sorted part의 직후의 element와 swap시키는 정렬
selectionSort(A[1 ... N], min, max): if max <= min: return min_index = min for i in [min ... max+1): if A[i] < A[min_index]: min_index = i swap A[min] and A[min_index] selectionSort(A, min+1, max)- Recursion, Iteration 두 가지 방법으로 구할 수 있다.
- 한번 호출 시 마다 sorted part에서의 element의 위치가 결정된다(loof invariant)
- time complexity: O(N²)
- selectionSort 함수는 한번 호출 시 Array의 size를 N이라 할 때 linear search를 통해 총 O(N)번의 비교 연산을 수행한다.
- selectionSort 함수는 총 N번 호출되며 i번째 호출 시 subArray 크기는 N-i이다.
3. Insertion Sort
: Array를 sorted part와 unsorted part로 나눈 뒤, i번째 stage에서 해당 시점의 unsorted part의 제일 왼쪽 element를 sorted part에 insert하는 정렬.
insertionSort(A[1 ... N], N): for i in [2 ... N]: for j in [i-1 ... 0] and A[j] > A[j+1]: swap A[j] and A[j+1]- 각각의 stage에서는 insertion을 통해 sort를 수행하고, 최종적으로 sorted part의 크기를 N으로 만든다.
- i번째 stage가 끝나면 A[0 ... i]가 sorted part가 된다(loof invariant)
- insertion: unsorted part의 제일 왼쪽 element를 sorted part의 오른쪽 원소부터 비교해가며 swap한다. 현재보다 작은 element가 발견될 경우 이후의 모든 element와는 비교할 필요가 없다.
- time complexity: O(N²)
- 거의 정렬된 Array를 정렬할 경우 빠른 성능을 보인다.
- 계속해서 인접한 element와의 비교 및 swap을 진행하기 때문에 참조 지역성의 원리를 잘 만족한다.
4. Merge Sort
: Array를 작은 subarray로 Divide하고, sorted된 subarray들을 Merge해가면서 전체 Array를 정렬.
mergeSort(A[1 ... N], left, right): if right <= left: return middle = (left + right) / 2 left = mergeSort(A, min, middle-1) right = mergeSort(A, middle, max) merge(A, left, middle, right) end merge(A[0 ... N], left, mid, right): l = mid - left + 1 r = right - mid allocate L[1 ... l] and R[1 ... r] for i = 1 to l: L[i] = A[left -1 + i] for j = 1 to r: R[i] = A[mid + j] L[l + 1] = R[r + 1] = INF i = 1 j = 1 for k = left to right: if L[i] <= R[j]: A[k] = L[i] i = i + 1 else: A[k] = R[j] j = j + 1 end- divide and conquer 알고리즘을 이용한 정렬.
- 인접한 덩어리를 merge하기에 참조 지역성의 원리를 잘 만족하지만 merge에서 할당하는 추가적인 공간 낭비가 심하다(Array size에 비례하게). in-place sorting이 아니다.
- size N인 array를 sort하는 시간 = (size가 n/2인 subarray를 merge sort) + (두 subarray를 merge하는 시간)
- T(n) = 2*T(n/2) + O(n) => time complexity: O(N logN)
5. Quick Sort
: pivot을 선정하여 기준으로 잡고 대소관계를 따져 subarray를 분할한 뒤 merge하는 정렬
quickSort(A[1 ... N], left, right): if right <= left: return else: pivot = partitioning(A, left, right) quickSort(left, pivot - 1) quickSort(pivot + 1, right) end partitioning(A[1 ... N], left, right): pivot = A[right] i = left - 1 for j = left to high - 1: if A[j] < pivot: i++ swap A[i] and A[j] swap A[i + 1] and A[right] return i + 1 end- pivot을 잘못 선정할 경우 recursion tree가 skewed binary tree(편향 이진 트리)의 형태를 띔
- size N인 array를 sort하는 이상적인(best-case) 시간 = (size가 n/2인 subarray를 quick sort) + (두 subarray를 merge하는 시간)
- time complexity: worst-case O(N²) / average-case O(N logN) -> pivot을 uniformly random하게 선정한다고 가정.
- bast-case에 해당하는 pivot인 median을 O(n)에 구하는 알고리즘인 Median of Medians Algorithm이 존재함(2jinishappy.tistory.com/127?category=903864)
Quick Select를 O(n)에 구현 가능한 Median of Medians 알고리즘
2jinishappy.tistory.com/124 Array의 k번째 작은 element 찾기 - QuickSelect 알고리즘 Size가 n인 int형 Array에서 k번째로 작은 element를 찾는 방법은 여러 가지가 있다. 가장 formal하게, 배열을 sort한 뒤..
2jinishappy.tistory.com
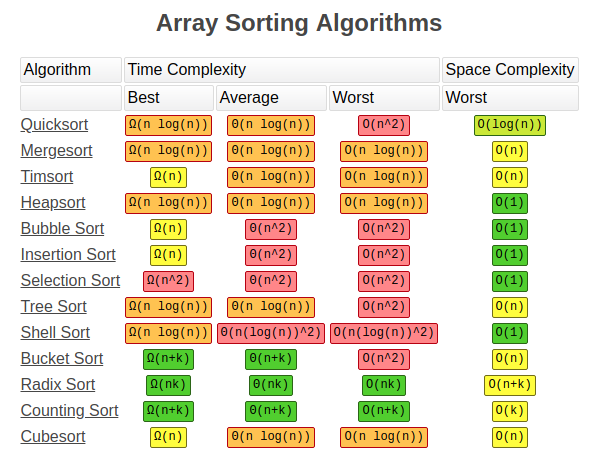
https://lamfo-unb.github.io/img/Sorting-algorithms/Complexity.png 해당 알고리즘들을 포함한 sort algorithm들의 best/average/worst case의 time complexity를 정리한 표 이다.
참고로 Java와 Python에서는 Insertion Sort와 Merge Sort를 결합한 Tim Sort 알고리즘을 Sort Algorithm으로 사용하고 있다.
'Algorithm' 카테고리의 다른 글
Connected Graph에서 MST를 생성하는 Kruskal's Algorithm(Greedy, Union Find) (413) 2021.03.16 무방향그래프에서의 Cut Vertex와 Biconnected Components (388) 2021.03.08 그래프의 Vertex를 정렬하는 Topological Sort - Kahn's Algorithm (0) 2021.02.15 [운영체제] LRU(Least Recently Used Algorithm) Algorithm이란? Python 구현 (0) 2021.02.05 Postfix Calculator(후위 표기식 계산기) 구현 (0) 2021.01.13