-
Connected Graph에서 MST를 생성하는 Kruskal's Algorithm(Greedy, Union Find)Algorithm 2021. 3. 16. 02:16
이전에 MST(Minimum Spanning Tree)에 대해 다룬 적이 있다.
Weighted Connected Graph에서는 edge의 cost 합이 최소가 되게 하는 Subgraph(Tree)를 구성할 수 있고, 이를 MST라고 한다.
이러한 MST를 생성하는 대표적인 알고리즘으로는 Kruskal(크루스칼), Prim(프림)알고리즘이 있다.
Kruskal's Algorithm(Greedy)
: 그래프 G의 MST를 이루는 edge set을 T라고 가정한다. 각 step마다 T에 추가해도 cycle이 생기지 않는 edge들 중 cost가 가장 작은 edge를 T에 추가한다. 이 과정을 MST가 완성될 때 까지 반복한다.
이와 같이 T에 새로운 edge e를 추가해도 spanning tree의 성질이 유지될 때 T+e는 feasible하다고 한다.
위의 알고리즘의 결과물은 반드시 Connected Graph(Tree)가 나오게 된다.
만약 T의 edge set으로 생성되는 그래프 G의 vertex set S에 속한 임의의 두 vertex u와 v가 unreachable하다고 가정하면, 크루스칼 알고리즘의 전제 조건인 Connected Graph에서 u에서 v로 향하는 path가 존재함에도(u에서 v가 reachable함에도) 해당 vertex들을 이어주는 edge를 추가해주지 않는 것이기에 크루스칼 알고리즘의 정의에 모순된다.
따라서 크루스칼 알고리즘으로 형성된 그래프의 Vertex들은 모두 connected하다.

크루스칼 알고리즘을 따라 MST를 형성하면 위의 그림과 같은 형태를 얻을 수 있다.
이 때 선택할 수 있는 edge가 1개 이상이라면(같은 cost를 가진 edge가 여러 개 라면) 아무 edge나 선택 가능하고, 이것을 기점으로 완성될 수 있는 MST는 여러 개가 존재할 수 있다.
그렇다면 edge를 선택할 때 왜 T에 추가했을 때 cycle이 생기지 않는 edge를 골라야 할까?
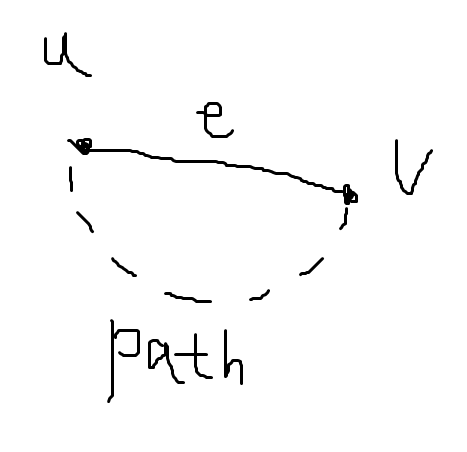
vertex u와 v가 있을 때, edge e를 추가해서 cycle이 생긴다는 것은, 이미 u에서 v로 reachable한 path가 존재한다는 것이다. 그리고 크루스칼 알고리즘의 정의에 의해 e는 u에서 v를 연결하는 path 내에 존재하는 모든 edge보다 weight이 클 수 밖에 없다(해당 edge들은 이미 edge set T에 있고, e보다 먼저 선택되었기 때문에 weight이 작을 수 밖에 없다).
이 때, path에 있는 edge이던 e이던 아무 edge를 삭제해도 여전히 u에서 v는 reachable하기 때문에 가장 weight가 큰 e가 삭제될 수 밖에 없다.
따라서 cycle이 생기는 edge를 추가하는 것은 Kruskal Algorithm의 성질 및 MST에 위배되는 것이다.
그리고 Kruskal's Algorithm의 중요한 성질 두 가지가 있다.
1️⃣ Kruskal's algorithm의 결과물 G' = (V(G), T)는 항상 Connected하다(feasibility).
: G'가 disconnected라고 가정하고 G의 connected component 집합을 {V1, V2, .. , Vn}이라 했을 때, G는 Connected graph라고 했으므로 V1상의 vertex와 V2상의 vertex를 잇는 edge가 무조건 존재한다. 그리고 이 edge e를 추가해도 graph는 acyclic 성질을 유지한다.
2️⃣ Kruskal's algorithm은 G의 edge들의 cost가 모두 다를 때 유일한 minimum spanning tree를 반환한다(optimality).
: T(Kruskal algorithm으로 얻어낸 edge set), T'(optimal solution으로 얻어낸 edge set)이 다르다고 가정한다. 그렇다면 T에 속하지 않는 edge e가 T'에만 속해있어야 한다. 위의 cycle을 증명했던 것과 유사하게, T에서 u-v path를 이루는 edge들의 cost는 모두 e보다 작다. 따라서 T'에서 e를 제거하고 e'(기존의 u-v path에 존재했던 edge)를 추가하는 것이 total cost가 기존보다 작으며 spanning tree를 이루게 되는데 이는 크루스칼 알고리즘의 정의에 위배된다(따라서 2번이 옳음이 증명된다).
Sort edges by weight and assume w1<=w2<=...<=wm T is empty (*T will store edges of a MST*) for i 1 to m do if T+i is feasible do (dose not contain cycle) add i to T return set T크루스칼 알고리즘을 구현한 수도코드이다.
해당 알고리즘의 time complexity는 O(m(n+m)) = O(m²)이 나오게 된다.
이후에 다시 Union-Find 자료구조를 이용한 크루스칼 알고리즘의 성능 향상을 업로드 해야겠다.
😴
+ 단순 greedy로 구현했을 때 O(m^2)의 시간복잡도를 가지는 것을 확인했다. 우리는 Union-Find 자료구조를 통해 크루스칼 알고리즘의 시간 복잡도를 줄일 수 있다.
Union-Find(2jinishappy.tistory.com/175) ?
Kruskal's algorithm의 과정을 다시 써보면 아래와 같다
1️⃣ 크루스칼 알고리즘의 중간 결과물들을 forest(tree들의 set)로 저장한다 => makeset
2️⃣ 새로 추가할 edge(cost가 가장 작은)가 forest 상의 두 tree T1, T2를 이어준다면 해당 edge를 추가해서 T1과 T2를 하나의 tree로 만들어 준다. => union
3️⃣ Edge가 같은 tree상의 두 vertex에 incident하면 해당 tree는 추가하지 않음(feasibility를 유지하기 위해) => find
파란색 글씨로 표시해준 부분은 Union Find 자료구조의 세 연산으로 구현해낼 수 있다
따라서 Kruskal's Algorithm을 Union Find를 사용해서 재 정의하면
1️⃣ 각 set들은 G의 vertex들로 이루어져 있고, 초기에는 모든 vertex가 본인만을 포함한 n개의 set을 가지고 있다.
2️⃣ 추가할 edge가 서로 다른 두 set에 속한 vertex와 incident하면, 두 set을 union한다(이 때 해당 edge를 MST의 edge set T에 추가. => 각 set에 속한 vertex들은 T에 의해 tree가 됨).
3️⃣ 어떤 edge가 서로 같은 두 set에 속한 vertex와 incident하면, 해당 edge는 추가하지 않는다.

출처: Algorithms - DASGUPTA pass compression을 적용한 Kruskal Algorithm의 수도 코드이다.
Time complexity:
make set n번 + edge sorting + find&union 최대 m번
= O(n) + O(m logn) + O(m logn) = O(m logn)
'Algorithm' 카테고리의 다른 글
Edge-Weighted Graph에서의 최단경로를 찾는 Dijkstra Algorithm (427) 2021.03.23 Connected Graph에서 MST를 생성하는 Prim's Algorithm(Greedy, Priority Queue) (412) 2021.03.19 무방향그래프에서의 Cut Vertex와 Biconnected Components (388) 2021.03.08 Sort Algorithm(Bubble/Insert/Selection/Merge/Quick)과 시간복잡도 (0) 2021.02.25 그래프의 Vertex를 정렬하는 Topological Sort - Kahn's Algorithm (0) 2021.02.15