Binary Tree에서 Height를 조절하기 위한 Tree Rotation

BST(Binary Search Tree)는 아래와 같은 편향 이진 트리(Skewed Binary Tree)일 경우, 성능이 악화된다

Complete Binary Tree일 때 탐색 시간복잡도는 O(log N)이지만, (최악의 경우) 연결리스트의 형태를 한 Skewed Binary Tree일 경우 시간 복잡도가 O(N)에 수렴한다

이러한 편향 현상은 BST에서 Insert, Delete 연산으로 인해 발생할 수 있어서, 이를 보완하기 위한 자료구조로 자가 균형 이진 탐색 트리(Self-Balanced Binary Search Tree)가 존재한다

그 대표적인 예시인 AVL Tree와 Red-Black Tree에서도 아래에서 소개할 Rotation 연산을 이용해서 스스로 Height 균형을 유지하기 때문에 Tree Rotation에 대해서만 따로 다뤄보려 한다

 

Tree Rotation

BST의 대표 성질(Node p에 대해 p의 left child의 값은 p보다 작고 right child의 값은 p보다 크다)를 해치지 않으면서 구조를 변경할 수 있는 연산이다

rotation 연산은 left rotation과 right rotation이 존재한다

왼쪽의 그림에서 Q를 기준으로 Right Rotation하면 오른쪽 형태가 되고, 다시 P를 기준으로 Left Rotation하면 왼쪽 형태가 된다

 

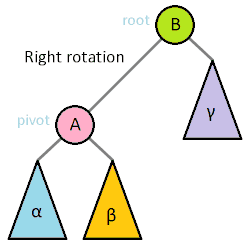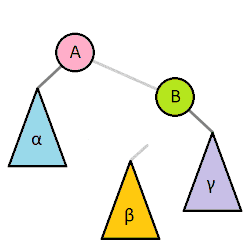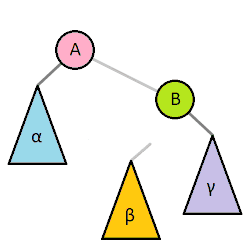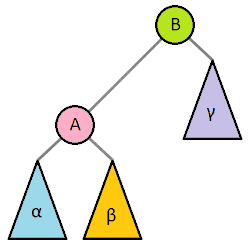
Right Rotation

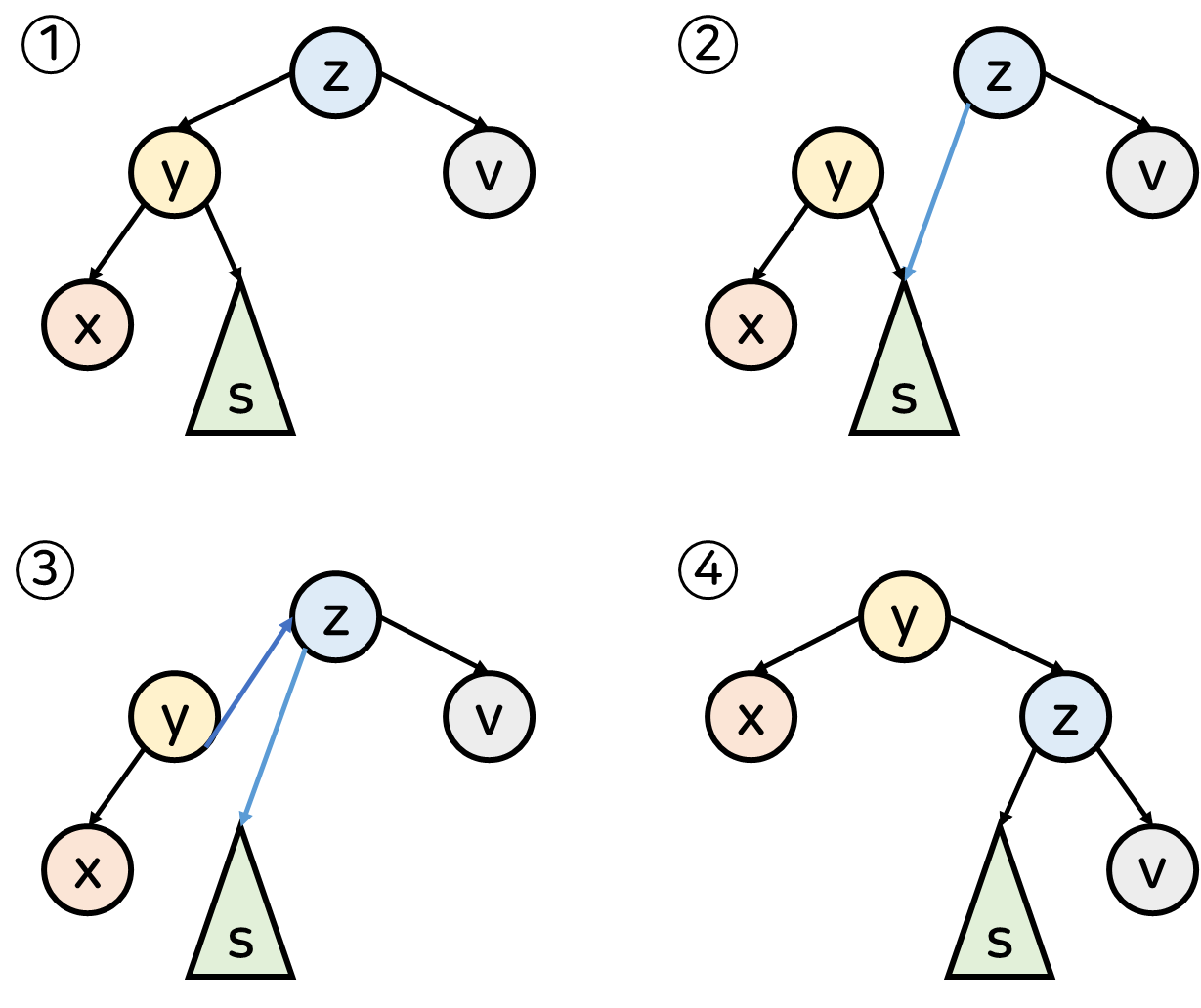
1️⃣ z를 기준으로 right rotation 하기 전 트리의 상태

2️⃣ z의 left child를 y의 right child(right subtree)로 변경

3️⃣ y의 right child를 z로 변경

4️⃣ 트리를 다시 그린 모습

 

Left Rotation

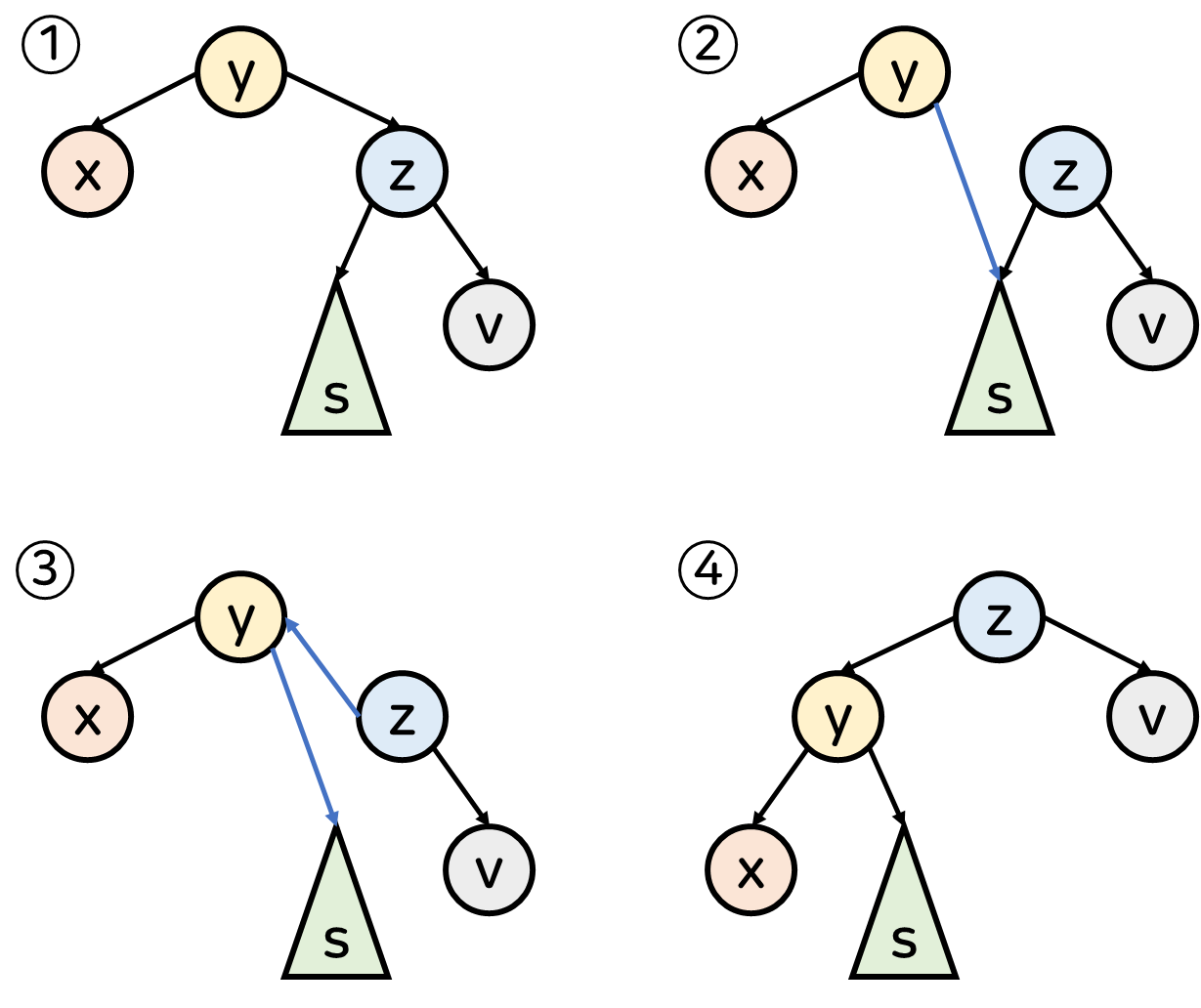
1️⃣ y를 기준으로 left rotation 하기 전 트리의 상태

2️⃣ y의 right child를 z의 left child(left subtree)로 변경

3️⃣ z의 left child를 y로 변경

4️⃣ 트리를 다시 그린 모습

 

이처럼 Left Rotation, Right Rotation 연산을 수행할 수 있고 이를 통해 Tree의 전체 Balance를 유지하는 데 활용된다

특정 Node p가 두 child를 가지고 있다고 할 때, height가 더 큰 child를 heavy child라고 한다

rotation 연산은 heavy child를 위로 올리고(height 감소), heavy가 아닌 child를 내려서(height 증가) subtree 간의 height 차이를 줄일 수 있다

이는 AVL Tree에서의 Self-Balancing 과정에서 활용된다